Deep Learning Fundamentals - Classic Edition

Backpropagation in Neural Networks

Hey, what's going on everyone? In this post, we're going to discuss backpropagation and what its role is in the training process of a neural network. Without further ado, let's get to it.

Stochastic gradient descent (SGD) review

We're going to be building on concepts that we covered in a couple of previous posts. These two posts covered what it means to train an artificial neural network, and how a network learns. If you haven't seen those yet, go ahead and check them out now, and then come back to this post once you finish up there.

We'll start out by first going over a quick recap of some of the points about stochastic gradient descent we learned in those posts. Then, we're going to talk about where backpropagation comes into the picture, and we'll spend the majority of our time discussing the intuition behind what backpropagation is actually doing.

In the previous posts we referenced, we discussed how, during training, stochastic gradient descent, or SGD, works to minimize the loss function by updating the weights with each epoch.

We mentioned how this updating occurs by calculating the gradient, or taking the derivative, of the loss function with respect to the weights in the model, but we didn't really elaborate on this point.

That's what we're going to discuss now. This act of calculating the gradients in order to update the weights actually occurs through a process called backpropagation.

Ok, so let's get ourselves set up.

Forward propagation

We have a sample arbitrary network here with two hidden layers. For simplicity, going forward with our explanation, we're going to be dealing with a single sample of input being supplied to our model, rather than a batch of input.

Now, as a quick refresher on the training process, remember that whenever we pass data to the model, we've seen that this data propagates forward through the network until it reaches the output layer.

Recall that each node in our model receives its input from the previous layer, and that this input is a weighted sum of the weights at each of the connections multiplied by the previous layer's output.

We pass this weighted sum to an activation function, and the result from this activation function is the output for a particular node and is then passed as part of the input for the nodes in the next layer. This happens for each layer in the network until we reach the output layer, and this process is called forward propagation.

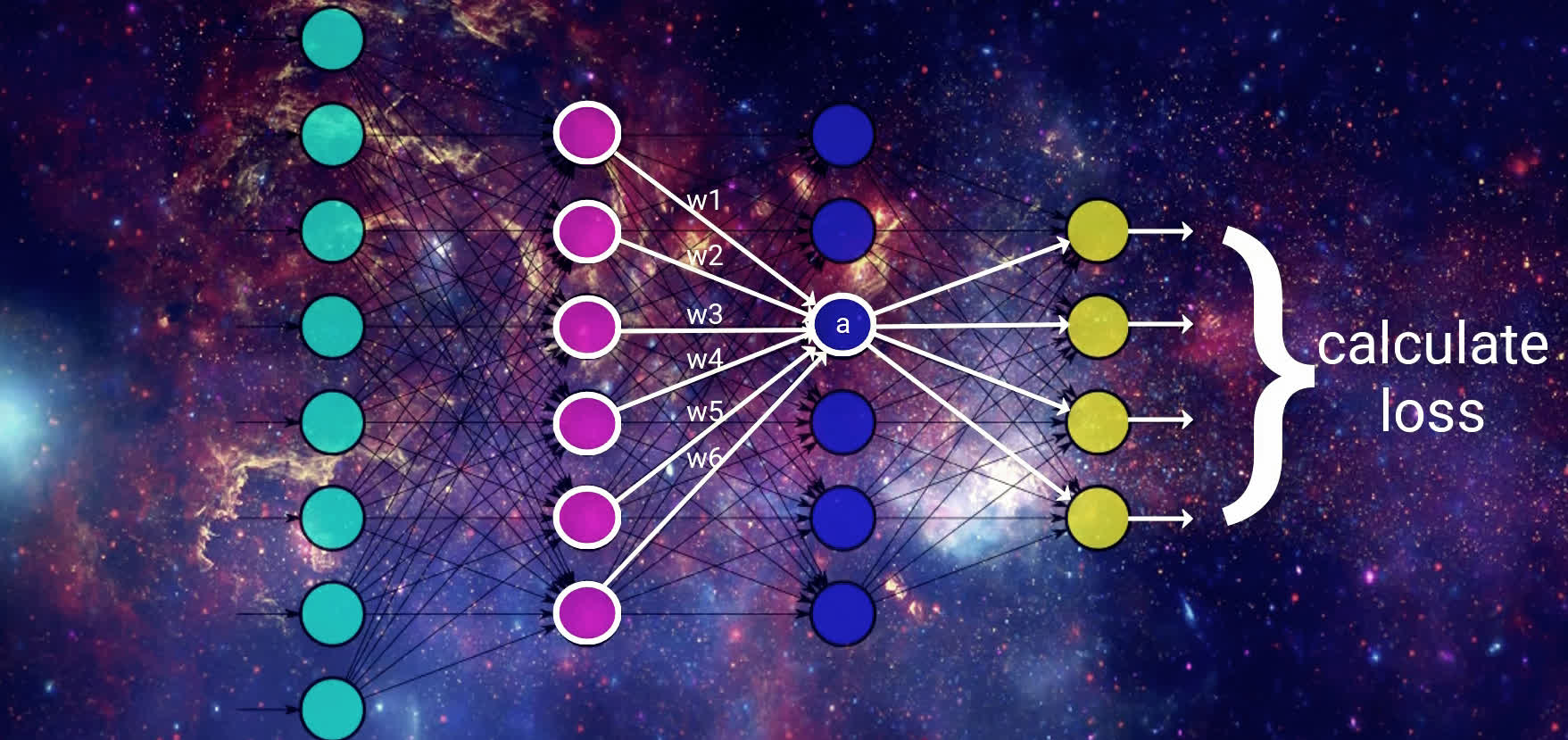
Once we reach the output layer, we obtain the resulting output from the model for the given input. If we're working to classify images of animals, for example, then each of the output nodes would correspond to a different type of animal, and the output node with the highest activation would be the output that the model thinks is the best match for the corresponding input.

Calculating the loss

Given the output results, we then calculate the loss on this result. The way the loss is calculated is going to depend on the particular loss function we're using, but for simplicity, let's just think of it for now as being how far off the model is on classifying the given input.

We can think of it as the difference between what the model predicted for a given input and what the given input actually is. We have a post on the loss function if you want to check that out further.

Alright, then, we've discussed how gradient descent's objective is to minimize this loss function. This is done by taking the derivative, that is, the gradient, of the loss function with respect to the weights in the model.

\[\frac{d\left( loss\right) }{d\left( weight\right) }\]

This is where backpropagation comes in.

As we mentioned, the process of moving the data forward through the network is called forward propagation. Given that the process we're about to cover is called backpropagation, you'd be correct in if you're thinking that this means we're somehow going to be working backwards through the network.

We have the output that was generated for our given input, the loss then gets calculated for that output, and now gradient descent starts updating our weights, using backpropagation, in order to minimize the loss function.

We're going to now focus on what backpropagation is doing by focusing on the intuition behind it.

Backpropagation intuition

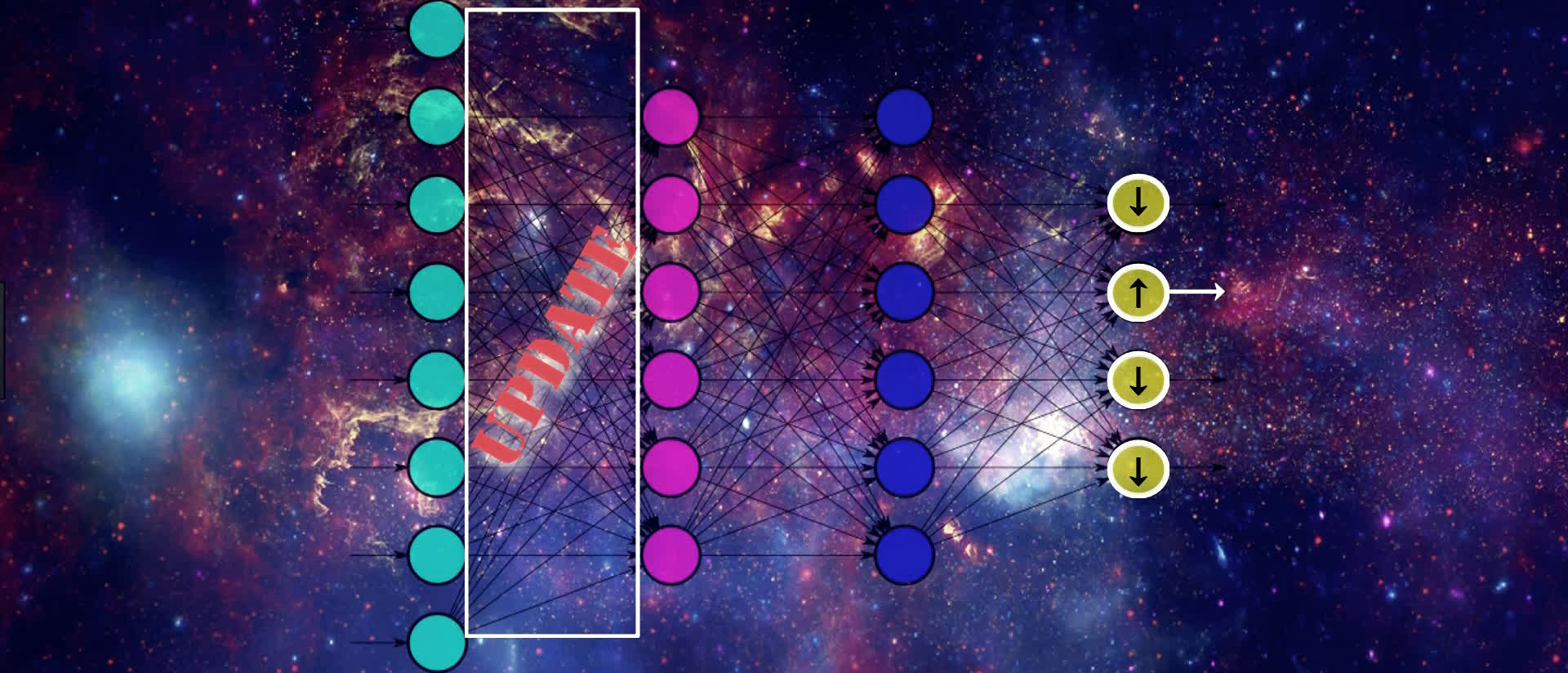
To update the weights, gradient descent is going to start by looking at the activation outputs from our output nodes.

Suppose that this output node here with the up arrow pictured below maps to the output that our given input actually corresponds to. If that's the case, then gradient descent understands that the value of this output should increase, and the values from all the other output nodes should decrease. Doing this will help SGD lower the loss for this input.

We know that the values of these output nodes come from the weighted sum of the weights for the connections in the output layer here being multiplied by the output from the previous layer and then passing this weighted sum to the output layer's activation function.

Therefore, if we want to update the values for the output nodes in the way we just discussed, one way to do this is by updating the weights for these connections that are connected to the output layer. Another way of doing this is by changing the activation output from the previous layer.

We can't actually directly change the activation output because it's a calculation based on the weights and the previous layer's output. But, we can indirectly influence a change in this layer's activation output by jumping backwards, and again, updating the weights here in the same way we just discussed for the output layer.

We continue this process until we reach the input layer. We don't want to change any of the values from the nodes in our input layer since this contains our actual input data.

As we can see, we're moving backwards through our network, updating the weights from right to left in order to slightly move the values from our output nodes in the direction that they should be going in order to help lower the loss.

This means that, for an individual sample, SGD is trying to increase the output value for the correct output node and decrease the output value for the incorrect output nodes, which, in turn, of course, decreases the loss.

It's also important to note, that in addition to updating weights to move in the desired direction i.e. positive or negative, backpropagation is also working to efficiently update the weights so that the updates are being done in a manner that helps to reduce the loss function most efficiently.

The proportion in which some weights are updated relative to others may be higher or lower, depending on how much affect the update is going to have on the network as a whole to lower the loss.

After calculating the derivatives, the weights are proportionally updated to their new values using the derivatives we obtain. The technical explanation for this update is shown in an earlier post.

We went through this example for a single input, but this exact same process will occur for all the input for each batch we provide to our network, and the resulting updates to the weights in the network are going to be the average updates that are calculated for each individual input.

These averaged results for each weight are indeed the corresponding gradient of our loss function with respect to each weight.

Summary of this process

Alright, we've done a lot, so let's give a quick summary of it all. When training an artificial neural network, we pass data into our model. The way this data flows through the model is via forward propagation where we're repeatedly calculating the weighted sum of the previous layers activation output with the corresponding weights, and then passing this sum to the next layer's activation function.

We do this until we reach the output layer. At this point, we calculate the loss on our output, and gradient descent then works to minimize this loss.

Gradient descent does this minimization process by first calculating the gradient of the loss function and then updating the weights in the network accordingly. To do the actual calculation of the gradient, gradient descent uses backpropagation.

Ok, so this covers the intuition behind what backpropagation is doing, but of course, this is all done with math behind the scenes.