Deep Learning Fundamentals - Classic Edition

Deep learning with convolutional neural networks

In this post, we'll be discussing convolutional neural networks. A convolutional neural network, also known as a CNN or ConvNet, is an artificial neural network that has so far been most popularly used for analyzing images for computer vision tasks.

Although image analysis has been the most wide spread use of CNNS, they can also be used for other data analysis or classification as well. Let's get started!

What is a CNN?

Most generally, we can think of a CNN as an artificial neural network that has some type of specialization for being able to pick out or detect patterns. This pattern detection is what makes CNNs so useful for image analysis.

If a CNN is just an artificial neural network, though, then what differentiates it from a standard multilayer perceptron or MLP?

CNNs have hidden layers called convolutional layers, and these layers are what make a CNN, well... a CNN!

CNNs can, and usually do, have other, non-convolutional layers as well, but the basis of a CNN is the convolutional layers.

Alright, so what do these convolutional layers do?

Convolutional layers

Just like any other layer, a convolutional layer receives input, transforms the input in some way, and then outputs the transformed input to the next layer. The inputs to convolutional layers are called input channels, and the outputs are called output channels.

With a convolutional layer, the transformation that occurs is called a convolution operation. This is the term that's used by the deep learning community anyway. Mathematically, the convolution operations performed by convolutional layers are actually called cross-correlations.

We'll come back to this operation in a bit. For now, let's look at a high level idea of what convolutional layers are doing.

Filters and convolution operations

As mentioned earlier, convolutional neural networks are able to detect patterns in images.

DEEPLIZARD Message notifications

Leaning Tip

Have you tried the DEEPLIZARD interactive convolution demo? It's designed to help you develop a deeper understanding of the convolution operation.

---

Try it now: Interactive Convolution Demo

With each convolutional layer, we need to specify the number of filters the layer should have. These filters are actually what detect the patterns.

Patterns

Let's expand on precisely what we mean When we say that the filters are able to detect patterns. Think about how much may be going on in any single image. Multiple edges, shapes, textures, objects, etc. These are what we mean by patterns.

• edges
• shapes
• textures
• curves
• objects
• colors

One type of pattern that a filter can detect in an image is edges, so this filter would be called an edge detector.

Aside from edges, some filters may detect corners. Some may detect circles. Others, squares. Now these simple, and kind of geometric, filters are what we'd see at the start of a convolutional neural network.

The deeper the network goes, the more sophisticated the filters become. In later layers, rather than edges and simple shapes, our filters may be able to detect specific objects like eyes, ears, hair or fur, feathers, scales, and beaks.

In even deeper layers, the filters are able to detect even more sophisticated objects like full dogs, cats, lizards, and birds.

To understand what's actually happening here with these convolutional layers and their respective filters, let's look at an example.

Filters (pattern detectors)

Suppose we have a convolutional neural network that is accepting images of handwritten digits (like from the MNIST data set) and our network is classifying them into their respective categories of whether the image is of a 1, 2, 3, etc.

Let's now assume that the first hidden layer in our model is a convolutional layer. As mentioned earlier, when adding a convolutional layer to a model, we also have to specify how many filters we want the layer to have.

A filter can technically just be thought of as a relatively small matrix ( tensor), for which, we decide the number of rows and columns this matrix has, and the values within this matrix are initialized with random numbers.

For this first convolutional layer of ours, we're going to specify that we want the layer to contain one filter of size 3 x 3.

Convolutional layer

Let's look at an example animation of the convolution operation:

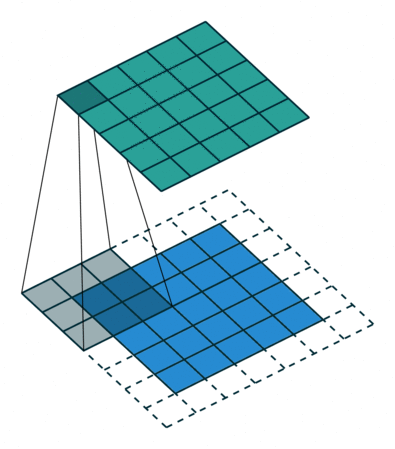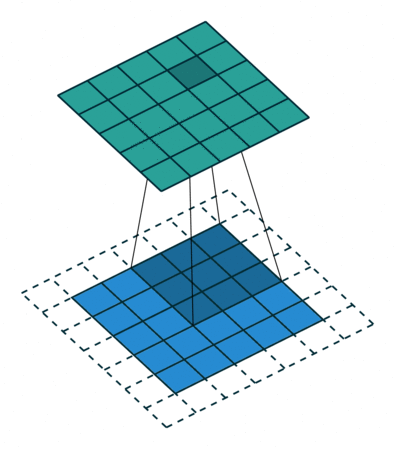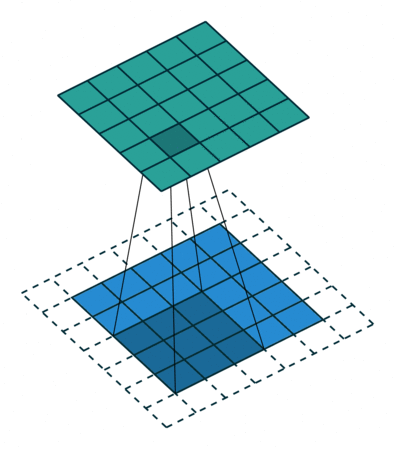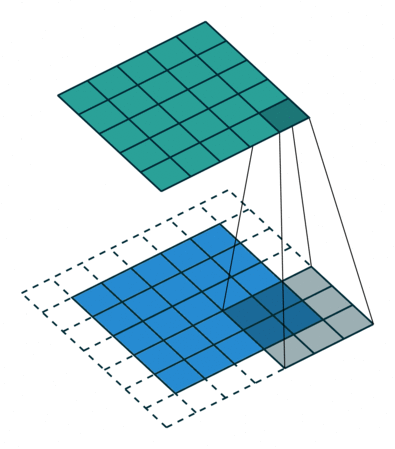
This animation showcases the convolution process without numbers. We have an input channel in blue on the bottom. A convolutional filter shaded on the bottom that is sliding across the input channel, and a green output channel:

• Blue (bottom) - Input channel
• Shaded (on top of blue) - 3 x 3 convolutional filter
• Green (top) - Output channel

For each position on the blue input channel, the 3 x 3 filter does a computation that maps the shaded part of the blue input channel to the corresponding shaded part of the green output channel.

This convolutional layer receives an input channel, and the filter will slide over each 3 x 3 set of pixels of the input itself until it's slid over every 3 x 3 block of pixels from the entire image.

Convolution operation

This sliding is referred to as convolving, so really, we should say that this filter is going to convolve across each 3 x 3 block of pixels from the input.

The blue input channel is a matrix representation of an image from the MNIST dataset. The values in this matrix are the individual pixels from the image. These images are grayscale images, and so we only have a single input channel.

• Grayscale images have a single color channel
• RGB images have three color channels

This input will be passed to a convolutional layer.

As just discussed, we've specified the first convolutional layer to only have one filter, and this filter is going to convolve across each 3 x 3 block of pixels from the input. When the filter lands on its first 3 x 3 block of pixels, the dot product of the filter itself with the 3 x 3 block of pixels from the input will be computed and stored. This will occur for each 3 x 3 block of pixels that the filter convolves.

For example, we take the dot product of the filter with the first 3 x 3 block of pixels, and then that result is stored in the output channel. Then, the filter slides to the next 3 x 3 block, computes the dot product, and stores the value as the next pixel in the output channel.

After this filter has convolved the entire input, we'll be left with a new representation of our input, which is now stored in the output channel. This output channel is called a feature map.

This green output channel becomes the input channel to the next layer as input, and then this process that we just went through with the filter will happen to this new output channel with the next layer's filters.

This was just a very simple illustration, but as mentioned earlier, we can think of these filters as pattern detectors.

A note about the usage of the "dot product"

We are loosely using the term "dot product" to discuss the operation done above, however, technically what we're actually doing is summing the element-wise products of each pair of elements in the two matrices.

For example, suppose we have two 3 x 3 matrices \(A\) and \(B\) as follows. $$A= \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix} $$ $$B= \begin{bmatrix} b_{1,1} & b_{1,2} & b_{1,3} \\ b_{2,1} & b_{2,2} & b_{2,3} \\ b_{3,1} & b_{3,2} & b_{3,3} \end{bmatrix} $$

Then, we sum the pairwise products like this: $$a_{1,1}b_{1,1}+a_{1,2}b_{1,2}+\cdots +a_{3,3}b_{3,3}$$

So, technically this operation is the summation of the element-wise products. Even so, you may still encounter the term "dot product" used loosely to refer to this operation. The reason for this is due to the fact that the operation shown here is an inner product, which is a generalization of the dot product. For this reason, you may also see this operation referred to as the Frobenius inner product or the summation of the Hadamard product as well.

Input and output channels

Suppose that this grayscale image (single color channel) of a seven from the MNIST data set is our input:

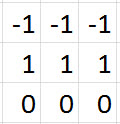
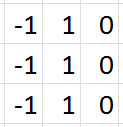
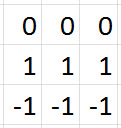
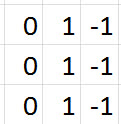
Let's suppose that we have four 3 x 3 filters for our first convolutional layer, and these filters are filled with the values you see below. These values can be represented visually by having -1s correspond to black, 1s correspond to white, and 0s correspond to grey.

Convolutional Layer with 4 filters

If we convolve our original image of a seven with each of these four filters individually, this is what the output would look like for each filter:

Output channels from the Convolutional Layer

We can see that all four of these filters are detecting edges. In the output channels, the brightest pixels can be interpreted as what the filter has detected. In the first one, we can see detects top horizontal edges of the seven, and that's indicated by the brightest pixels (white).

The second detects left vertical edges, again being displayed with the brightest pixels. The third detects bottom horizontal edges, and the fourth detects right vertical edges.

These filters, as we mentioned before, are really basic and just detect edges. These are filters we may see towards the start of a convolutional neural network. More complex filters would be located deeper in the network and would gradually be able to detect more sophisticated patterns like the ones shown here:

We can see the shapes that the filters on the left detected from the images on the right. We can see circles, curves and corners. As we go further into our layers, the filters are able to detect much more complex patterns like dog faces or bird legs shown here:

The amazing thing is that the pattern detectors are derived automatically by the network. The filter values start out with random values, and the values change as the network learns during training. The pattern detecting capability of the filters emerges automatically.

In the past, computer vision experts would develop filters (pattern detectors) manually. One example of this is the Sobel filter, an edge detector. However, with deep learning, we can learn these filters automatically using neural networks!

Wrapping up

Now, if you're interested in seeing how to work with CNNs in code, then check out the CNN and fine-tuning posts in the Keras series, or build a neural network from scratch with PyTorch in this series.

We should now have a basic understanding of convolutional neural networks, how these networks are made up of convolutional layers that themselves contain filters. I'll see you in the next one!