PyTorch - Python Deep Learning Neural Network API

CNN tensor input shape and feature maps

Welcome back to this series on neural network programming. In this post, we will look at a practical example that demonstrates the use of the tensor concepts rank, axes, and shape.

To do this, we'll consider a tensor input to a convolutional neural network. Without further ado, let's get started.

Convolutional Neural Network

In this neural network programming series, we are working our way up to building a convolutional neural network (CNN), so let's look at a tensor input for a CNN.

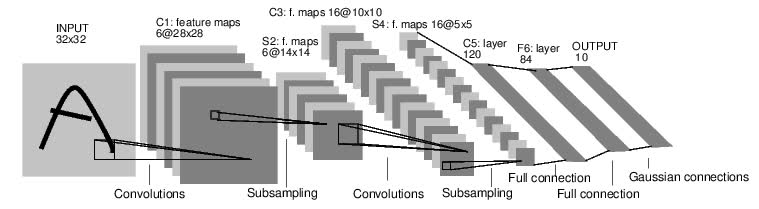
In the last two posts, we introduced tensors and the fundamental tensor attributes rank, axes, and shape. If you haven't seen those posts yet, I highly recommend you check them out.

What I want to do now is put the concepts of rank, axes, and shape to use with a practical example. To do this, we'll consider an image input as a tensor to a CNN.

Convolutional neural networks are the go-to networks for image recognition tasks because they are well suited for detecting spacial patterns.

Remember that the shape of a tensor encodes all the relevant information about a tensor's axes, rank, and indexes, so we'll consider the shape in our example, and this will enable us to work out the other values. Let's begin.

Shape of a CNN input

The shape of a CNN input typically has a length of four. This means that we have a rank-4 tensor with four axes. Each index in the tensor's shape represents a specific axis, and the value at each index gives us the length of the corresponding axis.

Each axis of a tensor usually represents some type of real world or logical feature of the input data. If we understand each of these features and their axis location within the tensor, then we can have a pretty good understanding of the tensor data structure overall.

To break this down, we'll work backwards, considering the axes from right to left. Remember, the last axis, which is where we'll start, is where the actual numbers or data values are located.

If we are running along the last axis and we stop to inspect an element there, we will be looking at a number. If we are running along any other axis, the elements are multidimensional arrays.

For images, the raw data comes in the form of pixels that are represented by a number and are laid out using two dimensions, height and width.

Image height and width

To represent two dimensions, we need two axes.

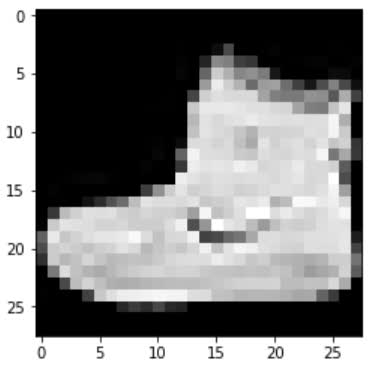
The image height and width are represented on the last two axes. Possible values here are 28 x 28, as will be the case for our image data in the fashion-MNIST dataset we'll be using in our CNN project, or the 224 x 224 image size that is used by VGG16 neural network, or any other image dimensions we can imagine.

Image color channels

The next axis represents the color channels. Typical values here are 3 for RGB images or 1 if we are working with grayscale images. This color channel interpretation only applies to the input tensor.

As we will reveal in a moment, the interpretation of this axis changes after the tensor passes through a convolutional layer.

Up to this point using the last three axes, we have represented a complete image as a tensor. We have the color channels and the height and width all laid out in tensor form using three axes.

In terms of accessing data at this point, we need three indexes. We choose a color channel, a height, and a width to arrive at a specific pixel value.

Image batches

This brings us to the first axis of the four which represents the batch size. In neural networks, we usually work with batches of samples opposed to single samples, so the length of this axis tells us how many samples are in our batch.

This allows us to see that an entire batch of images is represented using a single rank-4 tensor.

Suppose we have the following shape [3, 1, 28, 28] for a given tensor. Using the shape, we can determine that we have a batch of three images.

Each image has a single color channel, and the image height and width are 28 x 28 respectively.

1. Batch size
2. Color channels
3. Height
4. Width

This gives us a single rank-4 tensor that will ultimately flow through our convolutional neural network.

Given a tensor of images like this, we can navigate to a specific pixel in a specific color channel of a specific image in the batch using four indexes.

NCHW vs NHWC vs CHWN

It's common when reading API documentation and academic papers to see the B replaced by an N. The N standing for number of samples in a batch.

Furthermore, another difference we often encounter in the wild is a reordering of the dimensions. Common orderings are as follows:

• NCHW
• NHWC
• CHWN

As we have seen, PyTorch uses NCHW, and it is the case that TensorFlow and Keras use NHWC by default (it can be configured). Ultimately, the choice of which one to use depends mainly on performance. Some libraries and algorithms are more suited to one or the other of these orderings.

Output channels and feature maps

Let's look at how the interpretation of the color channel axis changes after the tensor is transformed by a convolutional layer.

Suppose we have a tensor that contains data from a single 28 x 28 grayscale image. This gives us the following tensor shape: [1, 1, 28, 28].

Now suppose this image is passed to our CNN and passes through the first convolutional layer. When this happens, the shape of our tensor and the underlying data will be changed by the convolution operation.

The convolution changes the height and width dimensions as well as the number of channels. The number of output channels changes based on the number of filters being used in the convolutional layer.

Suppose we have three convolutional filters, and lets just see what happens to the channel axis.

Since we have three convolutional filters, we will have three channel outputs from the convolutional layer. These channels are outputs from the convolutional layer, hence the name output channels opposed to color channels.

Each of the three filters convolves the original single input channel producing three output channels. The output channels are still comprised of pixels, but the pixels have been modified by the convolution operation. Depending on the size of the filter, the height and width dimensions of the output will change also, but we'll leave those details for a future post.

Feature maps

With the output channels, we no longer have color channels, but modified channels that we call feature maps. These so-called feature maps are the outputs of the convolutions that take place using the input color channels and the convolutional filters.

The word “feature” is used because the outputs represent particular features from the image, like edges for example, and these mappings emerge as the network learns during the training process and become more complex as we move deeper into the network.

Wrapping up

We should now have a good understanding of the overall shape of an input tensor to a CNN, and how the concepts of rank, axes, and shape apply to this understanding.

We'll deepen our understanding of these concepts in future posts when we begin building our CNN. Until then, I'll see you in the next one!