PyTorch - Python Deep Learning Neural Network API

Deep Learning Course 4 of 7 - Level: Intermediate

Callable Neural Networks - Linear Layers in Depth

video

lock
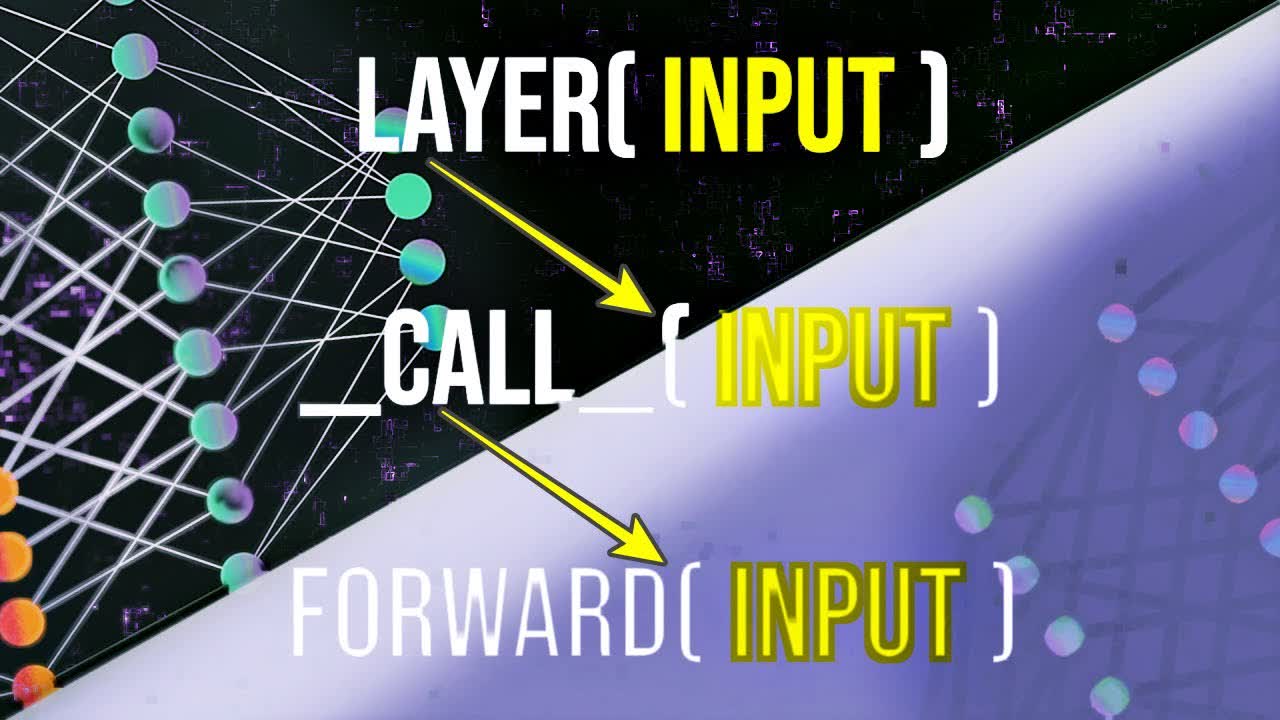
Lesson thumbnail for Callable Neural Networks - Linear Layers in Depth

text

lock

PyTorch Callable Neural Networks - Deep Learning in Python

Welcome to this series on neural network programming with PyTorch. In this one, we'll learn about how PyTorch neural network modules are callable, what this means, and how it informs us about how our network and layer forward methods are called.

Without further ado, let's get started.

quiz

lock

resources

lock
In this post, we'll be examining how and why we call PyTorch networks and layers. We'll also be diving into the inner workings of linear layers, the math and the code! 🕒🦎 VIDEO SECTIONS 🦎🕒 00:00 Welcome to DEEPLIZARD - Go to deeplizard.com for learning resources 00:30 Help deeplizard add video timestamps - See example in the description 12:51 Collective Intelligence and the DEEPLIZARD HIVEMIND 💥🦎 DEEPLIZARD COMMUNITY RESOURCES 🦎💥 👋 Hey, we're Chris and Mandy, the creators of deeplizard! 👀 CHECK OUT OUR VLOG: 🔗 https://youtube.com/deeplizardvlog 👉 Check out the website for more learning material: 🔗 https://deeplizard.com 💻 ENROLL TO GET DOWNLOAD ACCESS TO CODE FILES 🔗 https://deeplizard.com/resources 🧠 Support collective intelligence, join the deeplizard hivemind: 🔗 https://deeplizard.com/hivemind 🧠 Use code DEEPLIZARD at checkout to receive 15% off your first Neurohacker order 👉 Use your receipt from Neurohacker to get a discount on deeplizard courses 🔗 https://neurohacker.com/shop?rfsn=6488344.d171c6 ❤️🦎 Special thanks to the following polymaths of the deeplizard hivemind: Tammy Mano Prime Ling Li 🚀 Boost collective intelligence by sharing this video on social media! 👀 Follow deeplizard: Our vlog: https://youtube.com/deeplizardvlog Facebook: https://facebook.com/deeplizard Instagram: https://instagram.com/deeplizard Twitter: https://twitter.com/deeplizard Patreon: https://patreon.com/deeplizard YouTube: https://youtube.com/deeplizard 🎓 Deep Learning with deeplizard: Deep Learning Dictionary - https://deeplizard.com/course/ddcpailzrd Deep Learning Fundamentals - https://deeplizard.com/course/dlcpailzrd Learn TensorFlow - https://deeplizard.com/course/tfcpailzrd Learn PyTorch - https://deeplizard.com/course/ptcpailzrd Natural Language Processing - https://deeplizard.com/course/txtcpailzrd Reinforcement Learning - https://deeplizard.com/course/rlcpailzrd Generative Adversarial Networks - https://deeplizard.com/course/gacpailzrd 🎓 Other Courses: DL Fundamentals Classic - https://deeplizard.com/learn/video/gZmobeGL0Yg Deep Learning Deployment - https://deeplizard.com/learn/video/SI1hVGvbbZ4 Data Science - https://deeplizard.com/learn/video/d11chG7Z-xk Trading - https://deeplizard.com/learn/video/ZpfCK_uHL9Y 🛒 Check out products deeplizard recommends on Amazon: 🔗 https://amazon.com/shop/deeplizard 🎵 deeplizard uses music by Kevin MacLeod 🔗 https://youtube.com/channel/UCSZXFhRIx6b0dFX3xS8L1yQ ❤️ Please use the knowledge gained from deeplizard content for good, not evil.

updates

lock
deeplizard logo DEEPLIZARD Message notifications

Update history for this page

Did you know you that deeplizard content is regularly updated and maintained?

  • Updated
  • Maintained

Spot something that needs to be updated? Don't hesitate to let us know. We'll fix it!

All relevant updates for the content on this page are listed below.